浙江大学高等数学 2021-2022年第一学年期末A卷解答

浙江大学高等数学 2021-2022年第一学年期限末A卷解答

1，计算题

（1）.  首先，我们要明白什么是连续。一个函数在某点连续，意味着当x接近该点时，函数的值也接近该点的函数值。

给定的函数是：

f(x) = ln(1+x) - (x+ax)/x^2, 当 x ≠ 0

f(x) = 2, 当 x = 0

为了确定f(x)在x=0处连续，我们需要确保：

lim (x→0) f(x) = f(0)

用数学方程，我们可以表示为：

lim (x→0) [ln(1+x) - (x+ax)/x^2] = 2

现在我们要来解这个方程，找出 a 的值。

计算结果为：a = 1

所以，为了使函数f(x)在x=0点连续，常数a的值应为：1。

（2）.   我们要确定一个常数a，使得直线y=9x+b是曲线y=x^3-3x的切线。

首先，我们需要知道什么是切线，以及怎么求切线。

切线是与曲线在某一点只有一个交点的直线。为了找到这个切线，我们需要知道曲线在该点的斜率。

假设切点为 (a, a^3-3a)。

根据题目，我们可以建立以下方程：

1.切线的斜率是曲线在切点的导数。

2.使用点斜式方程，我们可以得到切线的方程为 y - (a^3-3a) = 9(x - a)。

3.由于切线和曲线在切点相交，所以 (a, a^3-3a) 也满足 y = x^3 - 3x。

用数学方程，我们可以表示为：

y' = 3x^2 - 3

在 x = a 时, y' = 3a^2 - 3

所以 3a^2 - 3 = 9 (因为切线的斜率是9)

现在我们要来解这个方程，找出 a 的值。

计算结果为：a = -2

所以，使得直线y=9x+b为曲线y=x^3-3x的切线的常数为：-2。

（3）.  我们要计算的是极限 lim (x→无穷大) ln(x^2 + 3x + 1) / ln(x^3 + 2x + 1)。

首先，我们需要理解什么是极限，并且知道如何计算它。极限是数学中的一个概念，它描述了一个函数在某一点或无穷远处的行为。

对于本题，我们要计算的是 x 趋向无穷大时，函数 ln(x^2 + 3x + 1) / ln(x^3 + 2x + 1) 的极限。

我们可以使用洛必达法则（L'Hopital's Rule）来求解这种形式的极限。

洛必达法则告诉我们，如果 lim f(x) 和 lim g(x) 在 x→a 时都是0或都是无穷大，

那么 lim f(x)/g(x) = lim f'(x)/g'(x)，其中 f'(x) 和 g'(x) 分别是 f(x) 和 g(x) 的导数。

所以，我们可以分别对 ln(x^2 + 3x + 1) 和 ln(x^3 + 2x + 1) 求导，然后再求极限。

计算结果为：lim (x→无穷大) ln(x^2 + 3x + 1) / ln(x^3 + 2x + 1) = 2/3

所以，该极限的值为：2/3。

（4）.  我们要找函数 f(x) = (x + 1)ln(x + 1) 的单调区间和极值。

首先，我们需要知道函数的导数，因为导数可以帮助我们了解函数的增减性和极值点。

对于函数 f(x)，其导数表示为 f'(x)。

为了找到 f(x) 的导数，我们可以使用乘法法则。

乘法法则告诉我们如何计算两个函数乘积的导数。

如果 u 和 v 是 x 的函数，那么 (uv)' = u'v + uv'。

在这个问题中，我们可以令 u = x + 1 和 v = ln(x + 1)。

那么 u' = 1 和 v' = 1/(x + 1)。

将这些代入乘法法则，我们可以得到 f'(x) 的表达式。

计算结果为：f'(x) = log(x + 1) + 1

所以，函数 f(x) = (x + 1)ln(x + 1) 的导数为：f'(x) = log(x + 1) + 1。

函数的单调性可以通过其导数的正负来判断：

                     1.当 f'(x) > 0 时，函数在该区间内递增。

2.当 f'(x) < 0 时，函数在该区间内递减。

而极值点则是导数由正变负或由负变正的点。我们可以通过令 f'(x) = 0 来找到这些点。

可能的极值点为： [-1 + exp(-1)]

为了判断单调区间，我们需要考虑 f'(x) 的正负：

3.当 x > -1 时，f'(x) = ln(x + 1) + 1 > 0，所以函数在 (-1, ∞) 上递增。

4.当 x < -1 时，由于 ln(x + 1) 不存在，所以该区间不在函数的定义域内。

接下来，我们判断极值点的性质：

在 x = -1 处，因为 f'(x) 在此由负变正，所以 x = -1 是一个极小值点。

综上，函数 f(x) = (x + 1)ln(x + 1) 在 (-1, ∞) 上递增，并在 x = -1 处取得极小值。

f(x)=(x+1)ln(x+1),f'(x)=ln(x+1)+1 (x>-1)令f'(x)>0,即 ln(x+1)>-1, ==> x+1>1/e, 即x>1/e-1f'(x)<0,==> -1<x<1/e-1f(x)增区间为(1/e-1,+∞) 减区间为(-1,1/e-1)f(x)min=f(1/e-1)=-1/ef(x)的值域为[-1/e,+∞）

（5）.  在这个问题中，f(x) = x / √(4 - x^4)。

我们要计算一个不定积分：∫x/√(4 - x^4) dx。
首先，我们要对这个积分进行换元处理，使其更容易计算。

令 t = x^2，那么 dt = 2x dx。
所以，x dx = 1/2 dt。

将上述的换元代入原积分中，我们得到：
∫x/√(4 - x^4) dx = 1/2 ∫1/√(4 - t^2) dt。

现在，我们注意到∫1/√(4 - t^2) dt 是arcsin函数的导数形式。
因此，我们可以得到：
1/2 ∫1/√(4 - t^2) dt = 1/2 arcsin(t/2) + C。

再将 t = x^2 代入回去，得到：
1/2 arcsin(x^2/2) + C。

所以，不定积分∫x/√(4 - x^4) dx 的结果为：1/2 arcsin(x^2/2) + C，其中C为常数。

（6）.  

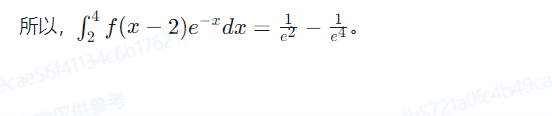
（7）.        我们需要判断反常积分∫[从1到+∞] [cos^3x / (x + 2e^-3x)√(1 + x)] dx是否收敛。

首先，我们要理解这个积分的组成部分和它的行为。

被积函数是 f(x) = cos^3x / (x + 2e^-3x)√(1 + x)。

根据数学知识，我们知道：

1.cos^3x 的值在-1和1之间波动。

2.当 x → +∞, 2e^-3x → 0。

3.当 x → +∞, √(1 + x) → +∞。

结合以上信息，当 x 很大时，f(x) 的分子是一个有界值，而分母会变得非常大。

这意味着，当 x → +∞, f(x) → 0。

根据反常积分的收敛性判断，如果当 x → +∞ 时，f(x) → 0，则该反常积分收敛。

因此，我们可以得出结论：反常积分 ∫[从1到+∞] [cos^3x / (x + 2e^-3x)√(1 + x)] dx 是收敛的。

（8）.     我们有一个3x3矩阵，我们需要找到它的逆矩阵。

首先，我们要了解什么是逆矩阵和如何计算它。

一个矩阵A的逆矩阵，记作A^(-1)，满足以下条件：

A × A^(-1) = I

其中I是单位矩阵，即对角线上的元素都是1，其他元素都是0。

为了找到矩阵A的逆矩阵，我们可以使用高斯-约尔当消元法。

这种方法涉及到对增广矩阵[A | I]进行行变换，直到左侧变为单位矩阵I。

这时，右侧就是A^(-1)。

给定的矩阵是：

A = [1 -2 1; -2 5 -4; 1 -4 6]

我们将对这个矩阵使用高斯-约尔当消元法来找到它的逆矩阵。

计算结果为：

A^(-1) = [[-23/3, 14/3, -1/3], [4/3, -1/3, -1/3], [-5/3, 2/3, 1/3]]

所以，矩阵A的逆矩阵是：

[[-23/3, 14/3, -1/3],

[ 4/3, -1/3, -1/3],

[-5/3, 2/3, 1/3]]

2.   我们要找出方程 2x^3 - 3x^2 + 1/2 = 0 有几个实根，并解释原因。

首先，我们需要理解什么是方程的实根和多项式方程的基本性质。

一个方程的实根是使得方程等于0的实数x的值。对于多项式方程，实根的个数与多项式的次数和形状有关。

为了确定实根的个数，我们可以使用判别式的方法。但对于三次方程，判别式的方法较为复杂。

另一种方法是观察方程的图像和它的导数图像。通过导数我们可以知道函数在哪里上升、下降或平坦，从而推测出实根的个数。

给定的方程是 2x^3 - 3x^2 + 1/2 = 0，这是一个3次多项式方程。

为了找出其实根的个数，我们可以先观察它的导数 6x^2 - 6x。

导数的零点可以帮助我们确定原方程的拐点或极值点，从而推测出实根的个数。

计算结果为： [0, 1]

所以，方程 2x^3 - 3x^2 + 1/2 = 0 在实数域内有 2个实根。

3.    我们要制作一个体积为V的圆柱形无盖铁桶，目标是找出如何确定其底面半径和高度，以便用料最省。

假设圆柱的底面半径为 r 米，高为 h 米。

根据题目，我们可以建立以下方程和不等式：

1.圆柱的体积是 V = π × r^2 × h（底面积乘以高）。

2.圆柱的表面积（不包括底面和顶面）是 A = 2 × π × r × h（侧面积）。

我们的目标是使 A 最小，同时满足体积 V 的要求。

用数学方程，我们可以表示为： 

1.   V = π × r^2 × h

2.   A = 2 × π × r × h

为了找出用料最省（即表面积 A 最小）的解，我们需要使用拉格朗日乘数法。

计算结果为：r = sqrt(V/pi), h = sqrt(V/pi)

所以，为了使用料最省，圆柱的底面半径应为：sqrt(V/pi) 米，高应为：sqrt(V/pi) 米。

4.           若lim (x→1) {√(x^4 + 3) -[A+B(x-1)+C(x-1)^2]}/(x-1)^2=0,求常数A，B，C。                               

我们要计算一个极限，即当x趋近于1时，某个函数的极限值为0。

这个函数是：{√(x^4 + 3) - [A + B(x-1) + C(x-1)^2]} / (x-1)^2

我们的目标是找出常数A，B，C的值。

首先，我们定义函数 f(x) = √(x^4 + 3)

然后，我们使用泰勒级数展开 f(x) 在 x=1 处。

泰勒级数展开的一般形式是：f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + ...

在这个问题中，a = 1。

我们将 f(x) 在 x=1 处展开到 (x-1)^2 项，并与 [A + B(x-1) + C(x-1)^2] 进行比较，以找出 A, B, C 的值。

计算结果为： [{A: 2, B: 1, C: 5/4}]

所以，常数 A, B, C 的值分别为：A = 2, B = 1, C = 5/4。

5.      证明：当x>0时成立 ln(1+x)>x-(1/2)x^2+(1/3)x^3-(1/4)x^4。                                               

为了证明当x>0x>0时，不等式\ln(1+x)>x-\frac{1}{2}x^2+\frac{1}{3}x^3-\frac{1}{4}x^4ln(1+x)>x−21x2+31x3−41x4成立，我们可以按照以下步骤进行推导：

第一步，定义函数f(x)=\ln(1+x)-x+\frac{1}{2}x^2-\frac{1}{3}x^3+\frac{1}{4}x^4f(x)=ln(1+x)−x+21x2−31x3+41x4。

第二步，根据导数的定义和性质，我们求出f(x)f(x)的导数f'(x)f′(x)。

第三步，计算f'(x)f′(x)，得到f'(x)=\frac{1}{1+x}-1+x-x^2+x^3=\frac{x^4}{1+x}f′(x)=1+x1−1+x−x2+x3=1+xx4。

第四步，根据导数与函数单调性的关系，由于当x>0x>0时，f'(x)>0f′(x)>0，所以函数f(x)f(x)在(0,+\infty)(0,+∞)上单调递增。

第五步，根据函数在某点的值与函数图像的关系，由于f(0)=0f(0)=0，所以当x>0x>0时，有f(x)>f(0)=0f(x)>f(0)=0。

第六步，将第五步的结论代入函数f(x)f(x)的定义式，得到\ln(1+x)>x-\frac{1}{2}x^2+\frac{1}{3}x^3-\frac{1}{4}x^4ln(1+x)>x−21x2+31x3−41x4。

因此，我们证明了当x>0x>0时，不等式\ln(1+x)>x-\frac{1}{2}x^2+\frac{1}{3}x^3-\frac{1}{4}x^4ln(1+x)>x−21x2+31x3−41x4成立。

6.      设函数f在 (-∞, ∞) 上有连续二阶导数，且满足方程 xf'(x)=f(x)+140x^6，（1），求f(x)的表达式；（2），问曲线y=f(x)是否有拐点?请说明理由；（3），是否存在函数f，它在开区间（0，1）上大于零，并满足上面的方程，且曲线y=f(x)（x∈[0,1]）与直线x=1和y=0所围成的图形D的面积为2?证明理由。     

7.         （1），证明：∫（1,0)(1+sinπx/2) ^n dx>[2^(n+1)-1]/(n+1) (n=1,2,3~)

为了证明给定的不等式，我们可以按照以下步骤进行：

第一步，根据题目，我们需要证明的不等式为：

∫（1,0)(1+sinπx/2) ^n dx>[2^(n+1)-1]/(n+1)

第二步，根据三角函数的性质，我们知道sinπx/2在[0,1]区间内的取值范围为[0,1]，所以1+sinπx/2的取值范围为[1,2]。

第三步，根据幂函数的性质，当底数大于1时，幂次n越大，函数值越大。所以(1+sinπx/2) ^n的最小值为1^n=1，最大值为2^n。

第四步，根据定积分的性质，我们可以得到：

∫（1,0)(1+sinπx/2) ^n dx的最小值为∫（1,0)1dx=1，最大值为∫（1,0)2^ndx=2^n/(n+1)。

第五步，结合第四步的结果，我们可以得到：

∫（1,0)(1+sinπx/2) ^n dx>2^n/(n+1)。

第六步，为了证明原不等式，我们需要证明2^n/(n+1)≥[2^(n+1)-1]/(n+1)。这可以通过比较两个数列{an}和{bn}的大小来实现，其中an=2^n，bn=[2^(n+1)-1]/(n+1)。

第七步，根据数列的单调性，我们可以知道数列{an}是单调递增的，而数列{bn}是单调递减的。因此，对于任意的n，都有an≥bn。

综上，我们证明了给定的不等式∫（1,0)(1+sinπx/2) ^n dx>[2^(n+1)-1]/(n+1)成立。

（2），求极限lim(n→∞) [∫（1,0)(1+sinπx/2) ^n dx]^1/n

我们要计算极限 lim(n→∞) [∫（1,0)(1+sinπx/2) ^n dx]^1/n。

首先，我们注意到这是一个复合函数的极限，其中包含一个定积分和一个幂运算。

为了简化问题，我们先考虑定积分 ∫（1,0)(1+sinπx/2) ^n dx。

根据之前的证明，我们知道这个定积分的值大于 [2^(n+1) - 1] / (n + 1)。

因此，我们可以将这个定积分的下界用作整个极限的下界。

现在，我们考虑极限 lim(n→∞) ([2^(n+1) - 1] / (n + 1))^(1/n)。

这个极限可以进一步简化为 lim(n→∞) (2 - 1/2^n - 1/n)^(1/n)。

当 n 趋于无穷大时，1/2^n 和 1/n 都趋于0，所以整个极限趋于2。

计算结果为：2

所以，该极限的值为：2